How it works

Sections referenced in the code are from the longer DBSP paper.

SQL → stepping terminology

Given the tables:

a     x: INT │ name: TEXT
     ────────┼─────────────
       24    │ Bob
       ...   │ ...

b     y: INT │ name: TEXT
     ────────┼─────────────
       3     │ Sue
       ...   │ ...

We can consider the SQL query:

SELECT a.x, b.y
FROM a
JOIN b USING (name)

as a function with the following type:

class A:
    x: int
    name: str

class B:
    y: int
    name: str

class Result:
    x: int
    y: int

def query(
    a: Table[A],
    b: Table[B],
) -> Table[Result]

We call query(a, b) (where a and b are tables of data at some point in time) and we get returned a Table of results. The first change in terminology we’re going to make is Table → ZSet

ZSets

ZSets are very similar to tables in SQL, but they also store the count of the value, so for example, given the table:

 x: INT │ name: TEXT
────────┼────────────
 24     │ Bob
 12     │ Sue
 24     │ Bob
 3      │ Bob
 ...    │ ...

We instead have the ZSet:

st.ZSetPython({
    A(x=24, name="Bob"): 2,
    A(x=12, name="Sue"): 1,
    A(x=3,  name="Bob"): 1,
})

Which has the __repr__:

<ZSetPython>
╭───────────┬─────┬────────╮
│   _count_ │   x │ name   │
├───────────┼─────┼────────┤
│         2 │  24 │ Bob    │
│         1 │   3 │ Bob    │
│         1 │  12 │ Sue    │
╰───────────┴─────┴────────╯

Storing tables as a bag makes sense, but why bother with the count?

Representing changes to the database

Remember our:

def query(a: Table[A], b: Table[B]) -> Table[Result]

The aim of Incremental View Maintenance is to be able to (efficiently) write the function:

def query(a: Changes[A], b: Changes[B]) -> Changes[Result]

Using ZSets, we have one type able to represent both the Table and the Changes. If we wanted to remove one row of table a – A(x=24, name="Bob") we just use a count of -1:

changes = query(
    st.ZSetPython({A(x=24, name"Bob"): -1}),
    st.ZSetPython(),  # No update to table `b`
})

Here are two methods on ZSet that we’ll refer to shortly (see them in the code), these do as you’d expect:

def __neg__(self) -> Self: ...
def __add__(self, other: ZSet[T]) -> Self: ...

>>> a = st.ZSetPython({A(x=24, name="Bob"): 1})
>>> b = st.ZSetPython({A(x=24, name="Bob"): 3, A(x=4, name="Steve"): -1})
>>> a + b
<ZSetPython>
╭───────────┬─────┬────────╮
│   _count_ │   x │ name   │
├───────────┼─────┼────────┤
│         4 │  24 │ Bob    │
│        -1 │   4 │ Steve  │
╰───────────┴─────┴────────╯
>>> b * 3
<ZSetPython>
╭───────────┬─────┬────────╮
│   _count_ │   x │ name   │
├───────────┼─────┼────────┤
│         9 │  24 │ Bob    │
│        -3 │   4 │ Steve  │
╰───────────┴─────┴────────╯

Before we move on to implementing query functions that operate on changes, we need to introduce two more concepts, delays and graphs.

Delays

delay is a function you call on a value that returns the previous value it was called with, it has the following signature:

def delay(a: T) -> T: ...

Let’s write a query that uses it:

def query_delay(a: st.ZSet[str]) -> st.ZSet[str]:
    delayed = st.delay(a)
    return delayed

Then let’s demonstrate its usage:

>>> graph = st.compile(query_delay)
>>> store = st.StorePython.from_graph(graph)

>>> st.iteration(store, graph, (st.ZSetPython({"first": 1}),))
st.ZSetPython()

>>> st.iteration(store, graph, (st.ZSetPython({"second": 1}),))
st.ZSetPython({"first": 1})

Note we had to st.compile(...) the query to run it. You might wonder, why go to all the trouble of compiling, why not just run the function as is – this should become apparent when we introduce integration.

Note also that we had to set up a Store as we needed somewhere to put the data that we called delay with previously – we’ll go into these more later. For now, it’s enough to know that we can trivially swap out this in-memory store for one that persists the data to Postgres or SQLite.

Graphs

To run a query with st.iteration(...), we needed a graph and a store. The graph we compiled above has type:

st.Graph[
    st.A1[st.ZSet[str]],
    st.A1[st.ZSet[str]],
]

Aθ is just a collection of arguments with length θ – waiting on mypy support for TypeVarTuple over here.

If we print query_delay, we’ll see something like:

Graph(
    vertices={
        <Path ...input_0>: <Vertex identity (ZSet[str]) -> ZSet[str]>,
        <Path ...delayed>: <Vertex delay (ZSet[str]) -> ZSet[str]>
    },
    input=[
        (<Path ...input_0>, 0)
    ],
    internal={
        (<Path ...input_0>, (<Path ...delayed>, 0)),
    },
    output=[
        <Path ...delayed>
    ],
    run_no_output=[]
)

The graph has a:

Map of Path to Vertex. This where all the vertices in the graph are, from here on they are referenced by their Path. Note that each path has a .inner that describes exactly where it’s from.
List of all the inputs. These are a tuple of a Path and 0 for the first argument, 1 for the second argument (in the case of binary vertices).
Set of all the internal edges. These are each a tuple of a Path, pointing to a (Path, 0|1) tuple.
List of output vertices.
List of vertices that we want to run, but we don’t use in the output.

A vertex has a fairly simple type, there are unary and binary ones, let’s look at a unary one:

class VertexUnary(Generic[T, V]):
    t: type[T]
    v: type[V]
    operator_kind: OperatorKind
    path: Path
    f: Callable[[T], V]

t is the input type, v is the output type, operator kind is add, delay, filter etc, path is effectively the unique name of the vertex, f is the function that it runs.

Now let’s look at a more interesting graph and write a .png file with a diagram of it:

def query_graph(a: st.ZSet[A], b: st.ZSet[B]) -> st.ZSet[st.Pair[A, B]]:
    a_uppered = st.map(a, f=_upper)
    joined = linear.join(
        a_uppered,
        b,
        on_left=st.Index.pick(A, lambda a: a.name),
        on_right=st.Index.pick(B, lambda b: b.name),
    )
    integrated = st.integrate(joined)
    return integrated

>>> graph = st.compile(query_graph)
>>> st.write_png(graph, "my-graph.png")

This gives us the following diagram:

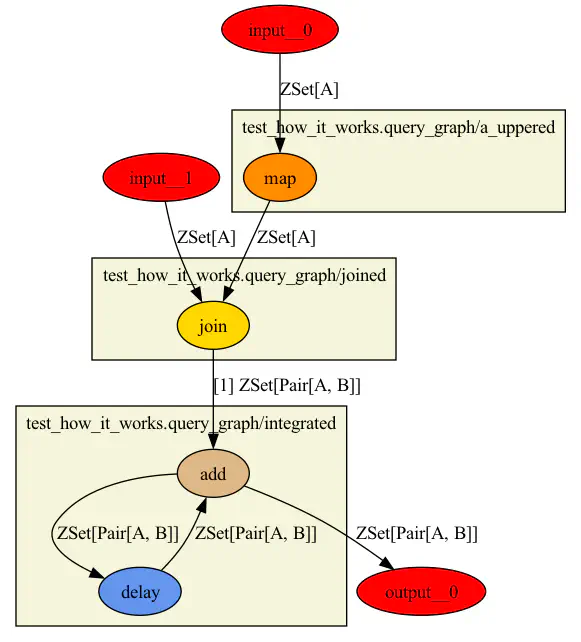
Hopefully it’s fairly obvious how that corresponds to the code of the query.

Incrementalizing a query

Right, we’re nearly ready to incrementalize a query – that is take a query that operates on whole tables, and convert it to one that operates on changes. Firstly, we’re going to introduce integration and differentiation. These are similar to the usual mathematical definitions: in the case of integrate(...), it will add up of all the values passed in between t=0 and t=now

Integration

Let’s look at how integration is defined in stepping:

def integrate(a: TAddable) -> TAddable:
    delayed: TAddable
    added = add(delayed, a)
    delayed = delay(added)
    return added

TAddable is anything with an __add__ method, that includes integers, floats, but also – as you’ll remember from previously – ZSets.

Then we say that added is the sum of the previous value and the input.

And that delayed is the previous added

Note that this isn’t runnable Python because of the loop between added and delayed – this is part of the reason for st.compile(...)

If we we run a query that just integrates, hopefully the results make sense:

def query_integrate(a: st.ZSet[str]) -> st.ZSet[str]:
    integrated = st.integrate(a)
    return integrated

>>> graph = st.compile(query_integrate)
>>> store = st.StorePython.from_graph(graph)

>>> st.iteration(store, graph, (st.ZSetPython({"a": 1}),))
st.ZSetPython({"a": 1})
>>> st.iteration(store, graph, (st.ZSetPython({"b": -1}),))
st.ZSetPython({"a": 1, "b": -1})
>>> st.iteration(store, graph, (st.ZSetPython({"a": 4}),))
st.ZSetPython({"a": 5, "b": -1})

Differentiation

Here’s the definition of differentiation:

def differentiate(a: TAddAndNegable) -> TAddAndNegable:
    delayed = delay(a)
    negged = neg(delayed)
    added = add(negged, a)
    return added

It does the inverse of integrate(...):

def query_differentiate(a: st.ZSet[str]) -> st.ZSet[str]:
    differentiated = st.differentiate(a)
    return differentiated

>>> graph = st.compile(query_differentiate)
>>> store = st.StorePython.from_graph(graph)

>>> st.iteration(store, graph, (st.ZSetPython({"a": 1}),))
st.ZSetPython({"a": 1})
>>> st.iteration(store, graph, (st.ZSetPython({"a": 1, "b": -1}),))
st.ZSetPython({"b": -1})
>>> st.iteration(store, graph, (st.ZSetPython({"a": 5, "b": -1}),))
st.ZSetPython({"a": 4})

Dumb Incrementalization

Given a query like:

def query_dumb(a: st.ZSet[A], b: st.ZSet[B]) -> st.ZSet[st.Pair[A, B]]:
    joined = linear.join(
        a,
        b,
        on_left=st.Index.pick(A, lambda a: a.name),
        on_right=st.Index.pick(B, lambda b: b.name),
    )
    return joined

The easy way for us to incrementalize the query is to wrap either end with an integrate and a differentiate:

def query_dumb(a: st.ZSet[A], b: st.ZSet[B]) -> st.ZSet[st.Pair[A, B]]:
    a_integrated = st.integrate(a)
    b_integrated = st.integrate(b)
    joined = linear.join(
        a_integrated,
        b_integrated,
        on_left=st.Index.pick(A, lambda a: a.name),
        on_right=st.Index.pick(B, lambda b: b.name),
    )
    differentiated = st.differentiate(joined)
    return differentiated

Let’s demonstrate that this does what we expect: Remember, the first item of the tuple gets passed into query_dumb(...) as a, the second as b

>>> st.iteration(store, graph, (
    st.ZSetPython({A(x=1, name="Bob"): 1, A(x=2, name="Jeff"): 1}),
    st.ZSetPython({B(y=3, name="Bob"): 1}),
))
╒═══════════╤════════════════════╤════════════════════╕
│   _count_ │ left               │ right              │
╞═══════════╪════════════════════╪════════════════════╡
│         1 │ A(x=1, name='Bob') │ B(y=3, name='Bob') │
╘═══════════╧════════════════════╧════════════════════╛

>>> st.iteration(store, graph, (
    st.ZSetPython(),
    st.ZSetPython({B(y=4, name="Bob"): 2}),
))
╒═══════════╤════════════════════╤════════════════════╕
│   _count_ │ left               │ right              │
╞═══════════╪════════════════════╪════════════════════╡
│         2 │ A(x=1, name='Bob') │ B(y=4, name='Bob') │
╘═══════════╧════════════════════╧════════════════════╛

>>> st.iteration(store, graph, (
    st.ZSetPython({A(x=1, name="Bob"): -1}),
    st.ZSetPython(),
))
╒═══════════╤════════════════════╤════════════════════╕
│   _count_ │ left               │ right              │
╞═══════════╪════════════════════╪════════════════════╡
│        -1 │ A(x=1, name='Bob') │ B(y=3, name='Bob') │
├───────────┼────────────────────┼────────────────────┤
│        -2 │ A(x=1, name='Bob') │ B(y=4, name='Bob') │
╘═══════════╧════════════════════╧════════════════════╛

As we add rows, we get returned the changes that need making to the output of the join query – including the removal of all the rows when we removed the left hand Bob.

The problem with this “dumb” incrementalization is that we end up integrating the entire tables in a_integrated and b_integrated, then joining together the entire tables, only to differentiate the results afterwards. This is pretty expensive to do, and we have to do it every iteration.

Incrementalizing map

With “linear” operators (see the DBSP paper for the definition), there is no need to do anything to the operator to incrementalize it, i.e. the incrementalized st.map(...) is just st.map(...).

The linear operators in stepping are:

st.add(...)
st.delay(...) (and variants)
st.delay_indexed(...)
st.differentiate(...)
st.filter(...)
st.haitch(...)
st.integrate(...) (and variants)
st.make_scalar(...)
st.make_set(...)
st.map(...)
st.map_many(...)
st.neg(...)

Incrementalizing join efficiently

Having written the “dumb” incrementalized join, we will now write the efficiently incrementalized version, it is defined in stepping as:

def join_lifted(
    l: ZSet[T],
    r: ZSet[U],
    *,
    on_left: Index[T, K],
    on_right: Index[U, K],
) -> ZSet[Pair[T, U]]:
    l_integrated = linear.integrate_indexed(l, indexes=(on_left,))
    r_integrated = linear.integrate_delay_indexed(r, indexes=(on_right,))
    joined_1 = linear.join(l_integrated, r, on_left=on_left, on_right=on_right)
    joined_2 = linear.join(l, r_integrated, on_left=on_left, on_right=on_right)
    added = linear.add(joined_1, joined_2)
    return added

We will discuss indexes below.

This is a result of Theorem 5.5 in the longer DBSP paper, namely that:

D(I(a) × I(b))

Is equivalent to:

I(a) × b + a × I(z⁻¹(b))

Or in stepping terminology:

differentiate(join(integrate(l), integrate(r)))

Which corresponds to the dumb definition above, is equivalent to:

join(integrate(l), r) + join(l, integrate(delay(r)))

Which corresponds to the efficient definition above.

Lifted functions

By default, stepping exports the following efficiently incrementalized operators (i.e. st.join refers to stepping.operators.lifted.join_lifted as opposed to stepping.operators.linear.join):

st.distinct(...)
st.count(...)
st.first_n(...)
st.group_reduce_flatten(...)
st.join(...)
st.outer_join(...)
st.reduce(...)
st.transitive_closure(...)

These should reference which Theorem they arise from in the DBSP paper in their respective docstrings.

Indexes

In the definition of join_lifted(...), there was mention of indexs. Indexes are used in various operations to enable quick look ups. For example in join_lifted(...), we want indexes on l_integrated and r_integrated as they will end up being large ZSets.

Indexes are a generic:

Index[T, K]

Where T is the same T from ZSet[T] and K is an Indexable key of T (including tuples of many keys). Indexes also have an ascending=True|False for each of the key(s).

Indexes are used to efficiently implement many things in stepping: joins, limits, grouping, distinct.

It is up to the class of ZSet as to how to implement indexes, for ZSetPython, we use a custom BTree class, for ZSetPostgres, we use Postgres’ built in indexing functionality.

It’s worth noting at this point how small the interface ZSet is, the only methods that need implementing are:

class ZSet(Protocol[T]):
    indexes: tuple[Index[T, Indexable], ...]

    def __neg__(self) -> Self: ...

    def __add__(self, other: ZSet[T]) -> Self: ...

    def iter(
        self,
        match: frozenset[T] | MatchAll
    ) -> Iterator[tuple[T, int]]: ...

    def iter_by_index(
        self,
        index: Index[T, K],
        match_keys: frozenset[K] | MatchAll
    ) -> Iterator[tuple[K, T, int]]: ...

This will make it pretty easy to swap out the storage layer in the future.

Cache

Caches are just a way for us to refer to delay ZSets after we’ve compiled a query, this means you can retrieve data from the Store at any time – useful for serving data over APIs for example. Example usage would be:

cache = st.Cache[X]()

def query(...):
    # ...
    y = cache[x](lambda x: st.integrate(x))
    # ...

graph = st.compile(query)
store = st.Store(...)
z = cache.zset(store)

Now z refers to the delay ZSet of the integrate.

The only two operators it seems reasonable to put after the lambda are those beginning st.integrate...(...), but the syntax is left open to do whatever.

Group

Let’s group some strings by their length:

class WithLen(st.Data):
    value: str
    length: int

def _len(s: str) -> WithLen: return WithLen(value=s, length=len(s))
def _zero_zset() -> st.ZSetPython[str]: return st.ZSetPython()
def _pick_zset(w: WithLen) -> st.ZSetPython[str]: return st.ZSetPython({w.value: 1})

def sum_by_length(a: st.ZSet[str]) -> st.ZSet[st.Pair[st.ZSetPython[str], int]]:
    with_len = st.map(a, f=_len)
    grouped = st.group_reduce_flatten(
        with_len,
        by=st.Index.pick(WithLen, lambda w: w.length),
        zero=_zero_zset,
        pick_value=_pick_zset,
    )
    return grouped

graph = st.compile(sum_by_length)
store = st.StorePython.from_graph(graph)
(action,) = st.actions(store, graph)

And test the query:

>>> action.insert("foo", "bar", "hullo")
╒═══════════╤═══════════════════════════╤═════════╕
│   _count_ │ left                      │   right │
╞═══════════╪═══════════════════════════╪═════════╡
│         1 │ <ZSetPython>              │       5 │
│           │ ╒═══════════╤═══════════╕ │         │
│           │ │   _count_ │ _value_   │ │         │
│           │ ╞═══════════╪═══════════╡ │         │
│           │ │         1 │ hullo     │ │         │
│           │ ╘═══════════╧═══════════╛ │         │
├───────────┼───────────────────────────┼─────────┤
│         1 │ <ZSetPython>              │       3 │
│           │ ╒═══════════╤═══════════╕ │         │
│           │ │   _count_ │ _value_   │ │         │
│           │ ╞═══════════╪═══════════╡ │         │
│           │ │         1 │ foo       │ │         │
│           │ ├───────────┼───────────┤ │         │
│           │ │         1 │ bar       │ │         │
│           │ ╘═══════════╧═══════════╛ │         │
╘═══════════╧═══════════════════════════╧═════════╛

Note the change we get returned when we remove "foo":

>>> action.remove("foo")
╒═══════════╤═══════════════════════════╤═════════╕
│   _count_ │ left                      │   right │
╞═══════════╪═══════════════════════════╪═════════╡
│        -1 │ <ZSetPython>              │       3 │
│           │ ╒═══════════╤═══════════╕ │         │
│           │ │   _count_ │ _value_   │ │         │
│           │ ╞═══════════╪═══════════╡ │         │
│           │ │         1 │ foo       │ │         │
│           │ ├───────────┼───────────┤ │         │
│           │ │         1 │ bar       │ │         │
│           │ ╘═══════════╧═══════════╛ │         │
├───────────┼───────────────────────────┼─────────┤
│         1 │ <ZSetPython>              │       3 │
│           │ ╒═══════════╤═══════════╕ │         │
│           │ │   _count_ │ _value_   │ │         │
│           │ ╞═══════════╪═══════════╡ │         │
│           │ │         1 │ bar       │ │         │
│           │ ╘═══════════╧═══════════╛ │         │
╘═══════════╧═══════════════════════════╧═════════╛

st.group_reduce_flatten(...) is implemented as follows:

grouped = group.group(a, by=by)
reduced = transform.per_group[grouped](
    lambda g: reduce_lifted(g, zero=zero, pick_value=pick_value)
)
flattened = group.flatten(reduced)

With the following types:

a: ZSet[T]
by: Index[T, K]
zero: def () -> TReducable
pick_value: def (T) -> TReducable
grouped: Grouped[ZSet[T], K]
reduced: Grouped[ZSet[TReducable], K]
flattened: ZSet[Pair[TReducable, K]]

Grouped[T, K] here is implemented basically as a dict[K, T].

transform.per_group[grouped](...) is a Transformer. In this case, that means that it takes the Graph compiled from reduce_lifted(...) and lifts all of the functions such that they operate per group (see the source for how this graph transformation takes place).

The output of all these transformations is a very scary looking graph:

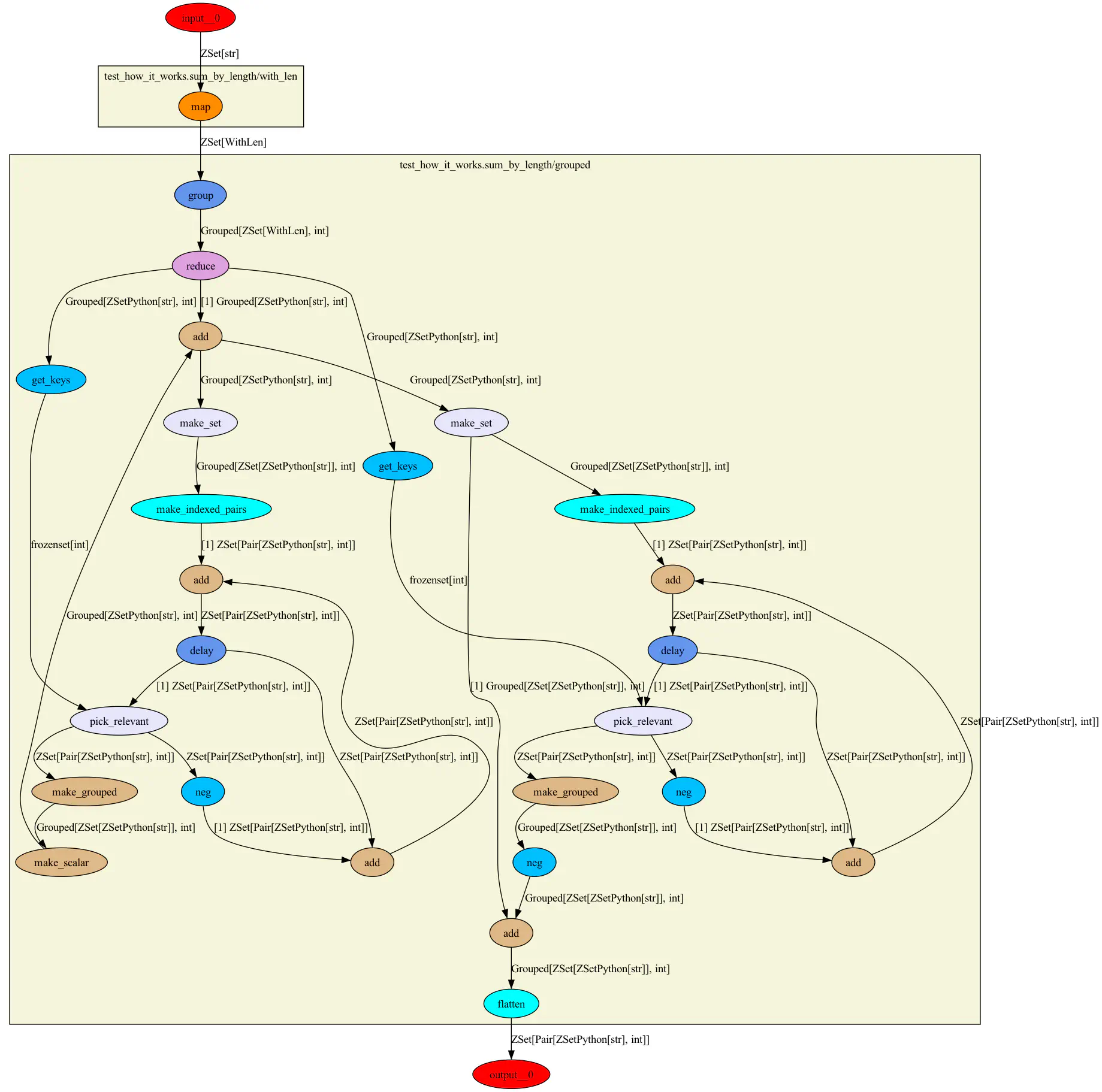
Unwritten

There are many more implementation details of stepping to talk about, these are placeholders in case I ever get round to writing them:

Go into more depth on the group transform.
Complete all of the operators.
ZSetSQL internals.
How does st.iteration(...) work.

How it works

SQL → stepping terminology #

ZSets #

Representing changes to the database #

Delays #

Graphs #

Incrementalizing a query #

Integration #

Differentiation #

Dumb Incrementalization #

Incrementalizing map #

Incrementalizing join efficiently #

Lifted functions #

Indexes #

Cache #

Group #

Unwritten #